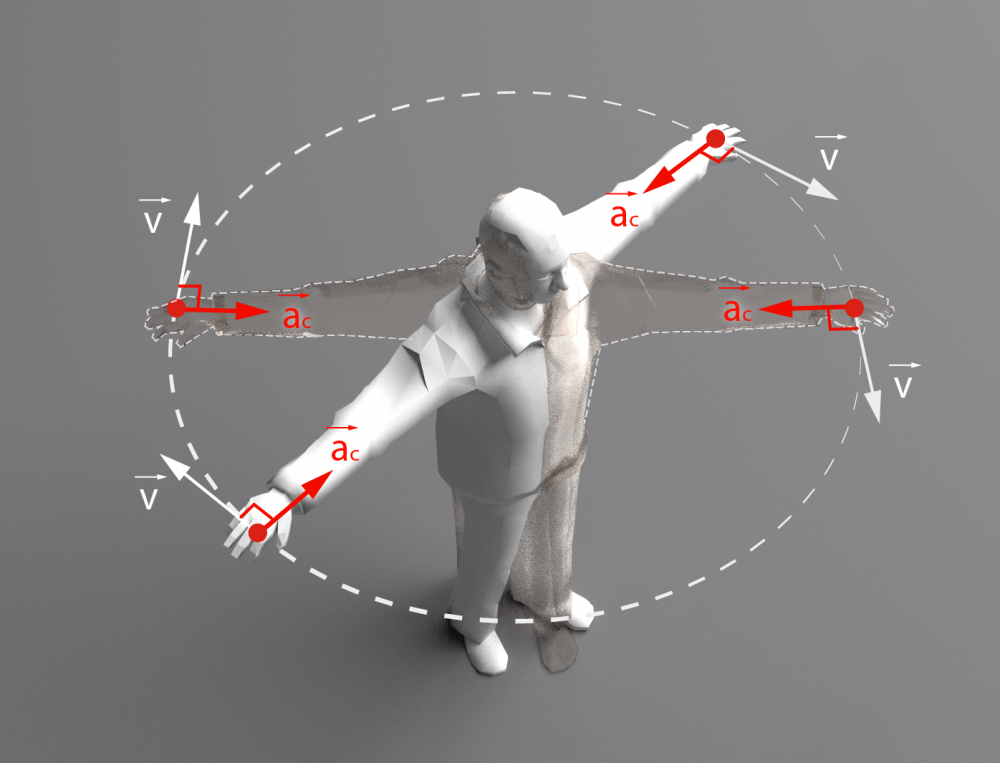
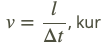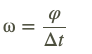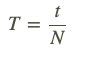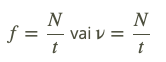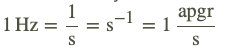Dabā svārstības ir izplatīts kustību veids. Svārstās vējā koki, ūdens svārstības, mūzikas instrumenta stīgas u.t.t. 
Par mehāniskām svārstībām sauc tādu kustību, kurā no stabila līdzsvara stāvokļa izvirzīts ķermenis periodiski atgriežas tajā.
Svārstību process raksturojas ar to, ka fizikālo raksturlielumu vērtības periodiski mainās. Dažādu ķermeņu svārstības ir atšķirīgas, tomēr visām svārstībām piemīt kopējas īpašības un to raksturlielumi ir svārstību periods, frekvence, amplitūda un enerģija Svārstību periods T ir laiks, kādā notiek viena pilna svārstība.

T – svārstību periods, s
t – svārstību laiks, s
n – svārstību skaits.

Svārstību skaits laika vienībā (sekundē) ir svārstību frekvence ν .

Svārstības, kas norisinās pēc kosinusa vai sinusa likuma, sauc par harmoniskām svārstībām.

Vilnis ir vides daļiņu mehānisko svārstību izplatīšanās process kādā vidē. Viļņus var izraisīt un novērot, piemēram, iemetot akmeni ūdenī. Uz ūdens virsmas veidojas koncentriski viļņu gredzeni, kas pārvietojas pa ūdens virsmu.

Ja ūdenī peld lapas vai citi nelieli priekšmeti, tad var redzēt, ka šie priekšmeti svārstās augšup un lejup, bet nepārvietojas kopā ar viļņiem. Tas rāda, ka ūdens virsmas slānis (šī ūdens slāņa daļiņas) svārstās augšup un lejup, bet nepārvietojas horizontālā virzienā. Šādas svārstības izplatās vidē viļņu veidā. Ja vides daļiņu svārstības sakrīt ar viļņa izplatīšanās virzienu, tad tādu vilni sauc par garenvilni.

Lai noskaidrotu no kā ir atkarīga ķermeņa impulsa izmaiņa, izdarīsim dažus 2. Ņūtona likuma formulas pārveidojumus. Tā kā spēka darbības virziens varētu būt arī pretējs kustības virzienam, tad vienādojumus rakstīsim projekciju formā:

1.Spēka impulss ir vienāds ar ķermeņa impulsa izmaiņu. 2. Ķermeņa impulsa izmaiņu var panākt:a) īslaicīgi iedarbojoties ar lielu spēkub) ilgākā laika intervālā iedarbojoties ar mazāku spēku. 3. Sadursmēs mijiedarbības spēka lielumu nosaka sadursmes laika intervāla Δt ilgums:

Leņķis starp abiem vektoriem ir vienāds ar 0°. Spēki ir paralēli un vērsti vienā virzienā, tad spēku moduļus saskaita. Aprēķiniem izmanto formulu Fkop=F1+F2

Spēki ir vektoriāli lielumi, jo tiem piemīt vērtība jeb modulis un tiem piemīt virziens. Tādēļ spēku saskaitīšanā izmanto vektoru saskaitīšanas likumus.

Piemērs:Divi bērni kopā velk ragavas, tādā veidā palīdzot viens otram. Tādēļ rezultējošais spēks vienmēr ir lielāks nekā katra bērna vilcējspēks atsevišķi.

2) Leņķis starp abiem vektoriem ir vienāds ar 180°. Spēki ir paralēli, bet pretēji vērsti, tad spēku moduļus savā starpā atņem. Kopspēka vērtība vienmēr ir pozitīva, jo starpību ieliek modulī. Aprēķiniem izmanto formuluFkop=|F1−F2|.

3) Leņķis starp abiem vektoriem ir vienāds ar 90°. Spēki ir savstarpēji perpendikulāri, tad kopspēka aprēķināšanai izmanto Pitagora teorēmu. Abi atsevišķie spēki ir kā taisnleņķa trijstūra katetes, bet kopspēks ir hipotenūza.  Aprēķiniem izmanto formulu Fkop=F21+F22−−−−−−−√. 

Ķermeņa vienmērīgā kustībā pa riņķa līniju mainās ātruma virziens. Lai mainītu ātruma virzienu, jāpieliek spēks. Savukārt nelīdzsvarots spēks ķermenim piešķir paātrinājumu ātruma izmaiņas virzienā (Otrais Ņūtona likums, par ko apgūsiet vēlāk).

a⃗ =v⃗ −v0→Δt=Δv−→Δt un virziens ir vektora Δv−→ virzienā.

Nevienmērīgu kustību gadījumā pārvietojumu aprēķina, izmantojot vidējā ātruma formulu: s=vvid.⋅Δt, kur

• s – pārvietojuma modulis (arī veiktais ceļš l), m,
• vvid. – kustības vidējais ātrums laika intervālā Δt.

Vienmērīgā ķermeņa kustībā pa riņķa līniju ātrums:

• nemaina  lielumu (moduli),
• maina virzienu,
• vērsts pa trajektorijas punkta pieskari,
• tiek saukts par lineāro ātrumu.

Tā kā kustība pa riņķa līniju ir vienmērīga, ātruma aprēķināšanai var izmantot vienmērīgas kustības ceļa formulu:

l  – ķermeņa veiktais ceļš pa riņķa līniju, vai loka garums, kuru ķermenis veicis laika intervālā Δt, nokļūstot no punkta 1punktā 2. 

Ja ir zināms apriņķošanas periods T jeb laika intervāls, kurā ķermenis veic vienu pilnu apgriezienu un riņķa līnijas rādiuss R, tad lineāro ātrumu var aprēķināt pēc sakarības:

Kustību pa riņķa līniju var raksturot arī ar leņķisko ātrumu. Leņķiskais ātrums ω rāda, par cik lielu leņķi pagriežas rotācijas rādiuss R laika vienībā. Ja laika intervālā Δt, materiālais punkts (ķermenis) no punkta 1 nonācis punktā 2, tad rotācijas rādiuss ir pagriezies par leņķi φ un leņķisko ātrumu varam aprēķināt pēc sakarības:

Vienmērīgā kustībā pa riņķa līniju nemainās ātruma modulis, bet izmainās ātruma virziens. Līdz ar to paliek nemainīgs arī laiks, kurā ķermenis veic vienu pilnu apgriezienu. Lai raksturotu vienmērīgu kustību pa riņķa līniju izmanto vairākus lielumus:

• apriņķošanas periods T – laiks, kurā ķermenis kustībā pa riņķa līniju veic vienu pilnu apgriezienu.

Ja kustības laikā t ķermenis veic N pilnus apgriezienus, tad apriņķošanas periodu T var aprēķināt pēc sakarības:

T mērvienība SI sistēmā – s (sekunde), bet praksē lieto arī citas.

• apriņķošanas frekvence f – apriņķojumu skaits laika vienībā (SI mērvienību sistēmā sekundē)

Ja kustības laikā t ķermenis veic N apgriezienus, tad apriņķošanas frekvenci f var aprēķināt pēc sakarības:

Frekvences mērvienība:[f]=1/s – šo vienību sauc par hercu un apzīmē ar Hz.

Salīdzinot apriņķošanas perioda un frekvences formulas, varam pamanīt, ka šie lielumi ir savstarpēji apgriezti:T=1/f un f=1/T 

Tehnikā bieži izmanto frekvences mērvienību apgriezienu skaits laika vienībā. Līdz ar to frekvences vienības pieraksts dažādās situācijās var būt dažāds:

Ja leņķu mērīšanu veicam SI sistēmas papildvienībās, tad jālieto mērvienība –  radiāns.

Leņķa lielumu radiānos var aprēķināt zinot riņķa līnijas rādiusu R un loka garumu l, kuru savelk dotais leņķis φ.

No šīs sakarības redzams, ka leņķis φ vienu vienību liels (1 radiāns) ir tad, ja leņķa savilktā loka garums ir vienāds ar riņķa līnijas rādiusu

Lietderības koeficients η ir lietderīgās jaudas N attiecība pret pilno jeb kopējo jaudu Np. Tā aprēķināšanai izmanto formulu

Lietderības koeficientam nav mērvienības. Bieži vien to izsaka procentos.Tā kā jauda ir paveiktais darbs noteiktā laika vienībā, tad lietderības koeficientu var izteikt kā lietderīgi pastrādātā darba

Lietderības koeficients vienmēr ir mazāks par 1 jeb 100% (η < 1 jeb η < 100%)